Tarjan의 SCC 분리 알고리즘 오류
1쇄 ~ 3쇄의 28.7절의 "강결합 컴포넌트 분리를 위한 타잔의 알고리즘"의 유도 과정과 코드에 오류가 있습니다. 유도 과정에서의 오류와 정정된 코드를 아래에서 보실 수 있습니다. 혼란을 드려 죄송합니다.
새로 쓴 부분을 여기에서 보실 수 있습니다.
교차 간선의 중요성
860쪽 마지막 문단("유의할 것은 교차 간선입니다." 로 시작)에서는 교차 간선을 무시해야 한다고 말하고 있습니다. 그러나 이것은 사실이 아닙니다. 어떤 정점이 같은 SCC 안의 정점과 연결되는 경로는 교차 간선을 통할 수도 있기 때문입니다.
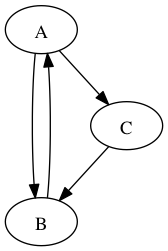
위 그래프가 이와 같은 반례의 예를 보여줍니다. A에서 깊이 우선 탐색을 시작해 B를 방문한 뒤, C를 방문했다고 합시다. A, B, C는 모두 같은 강결합 컴포넌트에 속하지만, 교차 간선을 무시할 경우 C는 컴포넌트의 다른 정점들과 연결되지 않으므로 책의 알고리즘은 C가 별도의 컴포넌트에 속한다고 잘못 판단하게 됩니다.
이와 같은 오류는 u에서 선조로 가는 경로에 반드시 존재해야 하는 역방향 간선이 반드시 u를 루트로 하는 서브트리에서 시작되어야 한다는 잘못된 가정에서 비롯됩니다. 이 가정은 본서에는 명시적으로 언급되어 있지 않습니다만, 교차 간선을 무시해도 된다는 결론에 암시적으로 반영되어 있습니다.
이 문제를 해결하기 위해서는 해당 간선이 교차 간선이라 하더라도 간선 반대편 정점이 현재 정점과 같은 SCC에 속할 가능성을 고려해야 합니다. 그러기 위해서는 간선 반대편 정점이 아직 별도의 SCC로 묶이지 않았어야 하고, 이것은 sccId[there]가 -1인지 확인하는 것으로 간편하게 확인할 수 있습니다.
이 때 깊이 우선 탐색 중 만나는 간선별로 알고리즘의 동작은 다음과 같이 나뉩니다.
- 트리 간선: 해당 간선을 따라 깊이 우선 탐색을 수행하고, 최소 발견 순서(
ret)를 갱신합니다. - 교차 간선: 간선의 반대쪽 끝 점이 아직 별도의 SCC로 묶이지 않았는지 확인하고, 들어있다면 최소 발견 순서(
ret)를 갱신합니다. - 역방향 간선: 최소 발견 순서(
ret)를 갱신합니다. - 순방향 간선: 무시합니다.
그런데 이것을 더 간단하게 만드는 것이 가능합니다. 간선 (here, there)가 역방향 간선인지 확인하기 위해 우리는 there에 대한 재귀호출이 끝나지 않았는지를 확인하지요. 그런데 (here, there)가 정말 역방향 간선이고 there에 대한 재귀호출이 끝나지 않았다면 there는 아직 별도의 SCC로 묶이지 않았을 겁니다. 따라서 sccId[there]가 -1인지 확인하는 것만으로 교차 간선과 역방향 간선을 모두 확인할 수 있습니다.
이 조건은 "자신보다 먼저 방문되었으면서도 아직 SCC로 묶이지 않은 정점으로 가는 간선이 있다면 현재 정점은 SCC의 루트일 수 없다"라고 해석할 수도 있지요.
다음은 고쳐진 코드 28.10을 보여줍니다.
// 그래프의 인접 리스트 표현
vector<vector<int> > adj;
// 각 정점의 컴포넌트 번호. 컴포넌트 번호는 0 부터 시작하며,
// 같은 강결합 컴포넌트에 속한 정점들의 컴포넌트 번호가 같다.
vector<int> sccId;
// 각 정점의 발견 순서와 scc() 종료 여부
vector<int> discovered, finished;
// 정점의 번호를 담는 스택
stack<int> st;
int sccCounter, vertexCounter;
// here 를 루트로 하는 서브트리에서 역방향 간선으로 닿을 수 있는 최소의 발견 순서를
// 반환한다.
int scc(int here) {
int ret = discovered[here] = vertexCounter++;
// 스택에 here 를 넣는다. here 의 후손들은 모두 스택에서 here 후에 들어간다.
st.push(here);
for(int i = 0; i < adj[here].size(); ++i) {
int there = adj[here][i];
// (here,there) 가 트리 간선
if(discovered[there] == -1)
ret = min(ret, scc(there));
// (here,there) 가 역방향이나 교차 간선
else if(discovered[there] < discovered[here] && sccId[there] == -1)
ret = min(ret, discovered[there]);
}
// here 가 강결합 컴포넌트의 루트인가 확인한다
if(ret == discovered[here]) {
// here 를 루트로 하는 서브트리에 남아 있는 정점들을 전부 하나의 컴포넌트로 묶는다
while(true) {
int t = st.top();
st.pop();
sccId[t] = sccCounter;
if(t == here) break;
}
++sccCounter;
}
finished[here] = 1;
return ret;
}
// tarjan 의 SCC 알고리즘
vector<int> tarjanSCC() {
// 배열들을 전부 초기화
sccId = discovered = vector<int>(adj.size(), -1);
finished = vector<int>(adj.size(), 0);
// 카운터 초기화
sccCounter = vertexCounter = 0;
// 모든 정점에 대해 scc() 호출
for(int i = 0; i < adj.size(); i++) if(discovered[i] == -1) scc(i);
return sccId;
}