프로그래밍 대회에서 배우는

알고리즘
문제 해결 전략

4.6 수행 시간 어림짐작하기

주먹구구 법칙

프로그래밍 대회의 시간 제한은 알고리즘의 시간 복잡도가 아니라 프로그램의 수행 시간을 기준으로 합니다. 따라서 어떤 알고리즘이 이 문제를 해결할 수 있을지 알기 위해서는 프로그램을 작성하기 전에 입력의 최대 크기와 알고리즘의 시간 복잡도를 보고 수행 시간을 어림짐작할 수 있어야 합니다. 물론 프로그램의 수행 시간을 짐작하는 것은 엄청나게 어려운 일입니다. 프로그램의 동작 속도에 영향을 끼치는 요소는 입력의 크기와 시간 복잡도를 제외하고도 엄청나게 많기 때문입니다. CPU의 클록 속도, 1클록마다 수행할 수 있는 CPU 명령어의 수, 프로그램의 메모리 접근 패턴, 운영 체제와 컴파일러의 버전, ... 목록을 만들자면 끝이 없습니다.

그러나 많은 경우에는 시간 복잡도와 입력 크기만 알고 있더라도 어떤 알고리즘이 시간 안에 동작할지 대략적으로 짐작하는 것이 가능합니다. 시간 복잡도는 프로그램의 수행 시간에 가장 큰 영향을 미치는 요소이기 때문입니다. 앞에서 언급한 요소들은 프로그램의 수행 속도를 기껏해야 몇 배씩 차이나게 할 뿐입니다. 그러나 알고리즘의 시간 복잡도가 달라지면 프로그램은 수천 배, 수만 배까지 빨라지거나 느려질 수 있습니다.

입력의 최대 크기 $N$이 10000이고, 테스트 케이스 하나를 푸는데 시간 제한이 1초인 문제를 풀고 있다고 가정합시다. 우리가 처음에 만든 알고리즘의 시간 복잡도가 $O(N^3)$이라고 하면, 과연 이 알고리즘으로 시간 내에 문제를 풀 수 있을까요? $O(N^2)$이나 $O(N \lg N)$은 어떨까요? 이런 질문에 대답하기 위해 많은 프로그래밍 대회 참가자들이 사용하는 주먹구구 법칙은 다음과 같습니다.

입력의 크기를 시간 복잡도에 대입해서 얻은 반복문 수행 횟수에 대해, 1초 당 반복문 수행 횟수가 1억($10^8$)을 넘어가면 시간 제한을 초과할 가능성이 있다.1

이 기준을 이용해 앞의 경우 각 알고리즘을 시간 안에 실행할 수 있을지 판단해 봅시다. $O(N^3)$ 알고리즘과 $O(N \lg N)$ 알고리즘은 쉽게 판단할 수 있습니다. $N^3$에 10000을 대입하면 1억을 훨씬 초과하고, $N \lg N$에 10000을 대입하면 1억에 훨씬 미치지 못하기 때문이지요. 그런데 $O(N^2)$ 알고리즘은 어떨까요? 1억을 초과하지 않으므로 시간 안에 실행될 거라고 말하고 싶지만, 경우에 따라 달라지기 때문에 프로그램을 직접 보기 전에는 뭐라고 말할 수 없습니다. 시간 복잡도와 입력의 크기 외의 요소들이 프로그램의 수행 속도를 열 배 정도는 쉽게 바꿔 놓을 수 있기 때문입니다. 이와 같이 이 법칙을 적용할 때는 충분한 여유를 두는 것이 좋습니다. 예를 들면 예측한 수행 횟수가 기준의 10% 이하인 경우와 기준의 10배를 넘는 경우에만 이 법칙을 적용하는 것이죠.

주먹구구 법칙은 주먹구구일 뿐이다

이 주먹구구 법칙은 수많은 가정 위에 지어진 사상누각이기 때문에, 절대로 맹신해서는 안 됩니다. 이 기준보다 느리지만 시간 안에 수행되는 프로그램이 얼마든지 있을 수 있고, 가끔은 이 기준보다 빠르지만 시간 안에 수행되지 않는 프로그램도 있기 때문입니다. 앞의 예에서 반복문 수행 횟수의 예측치가 기준에 가까운 $O(N^2)$ 알고리즘의 경우 시간 복잡도 외에도 다른 요소들을 참조해 시간 안에 수행될지를 판단해야 합니다. 이때 고려해야 하는 요소로 다음과 같은 것들이 있습니다.

  • ᆞ시간 복잡도가 프로그램의 실제 수행 속도를 반영하지 못하는 경우: O 표기법으로 시간 복잡도를 표현할 때는 상수나 최고차항 이외의 항들을 모두 지워 버립니다. 따라서 시간 복잡도 식에 입력의 최대 크기를 대입한 결과는 어디까지나 적당한 예측 값일 뿐입니다. 실제 프로그램이 수행하는 반복문의 수는 이 계산의 다섯 배일 수도 있고, 10분의 1일 수도 있습니다.
  • ᆞ반복문의 내부가 복잡한경우: 반복문 내부는 단순하면 단순할수록 좋습니다. 반복문의 내부가 길거나, 시간이 많이 걸리는 연산(실수 연산, 파일 입출력 등)을 많이 사용할 경우에는 이 가정보다 시간이 오래 걸릴 수밖에 없지요. 반대로 반복문의 내부가 아주 단순한 경우에는 이 가정보다 프로그램이 빨리 수행될 겁니다.
  • ᆞ메모리 사용 패턴이 복잡한 경우: 현대의 CPU는 메모리에 있는 자료를 직접 접근하는 대신 캐시라고 부르는 작고 빠른 메모리로 옮겨온 뒤 처리합니다. 메모리에서 캐시로 자료를 가져올 때는 인접한 자료들을 함께 가져오기 때문에, 인접한 자료들을 연속해서 사용하는 프로그램은 메모리에서 매번 자료를 가져올 필요 없이 캐시에 이미 저장된 자료를 사용하게 됩니다. 이런 차이는 시간 복잡도에는 아무 영향을 미치지 않지만 프로그램의 실제 수행 속도는 훨씬 빨라지게 됩니다.
  • ᆞ언어와 컴파일러의 차이: 앞의 법칙은 최적화 옵션을 켠 현대 C++ 컴파일러를 기준으로 합니다. 만약 최적화 옵션이 꺼져 있거나, 그보다 느린 언어를 사용한다면 수행 시간이 더 걸릴 수밖에 없습니다.
  • ᆞ구형 컴퓨터를 사용하는 경우: 이건 너무나 당연하지요. 위의 법칙은 대략 지 난 4~5년 사이에 출시된 CPU들을 기준으로 합니다.

이렇게 실제 알고리즘과 프로그램 구현을 참조해 속도를 어림짐작할 때는 평소에 작성하는 프로그램들의 시간 복잡도와 수행 시간의 상관 관계에 대한 경험과 직관이 있으면 큰 도움이 됩니다.

실제 적용해 보기

1차원 배열에서 연속된 부분 구간 중 그 합이 최대인 구간을 찾는 문제를 풀어 봅시다. 예를 들어 배열 [-7, 4, -3, 6, 3, -8, 3, 4]에서 최대 합을 갖는 부분 구간은 [4, -3, 6, 3]으로 그 합은 10입니다. 이 문제는 여러 가지 알고리즘으로 해결할 수 있는 것으로 유명하지요. 여기에서는 시간 복잡도가 서로 다른 여러 알고리즘을 구현하고 각 알고리즘의 수행 시간이 어떻게 다른지 확인해 보겠습니다.

첫 번째로 다룰 알고리즘은 주어진 배열의 모든 부분 구간을 순회하면서 그 합을 계산하는 알고리즘입니다. 코드 4.9의 inefficientMaxSum()이 이 구현을 보여줍니다. 이 알고리즘은 $O(N^2)$개의 후보 구간을 검사하고, 각 구간의 합을 구하는 데 $O(N)$의 시간이 걸리기 때문에 이 알고리즘의 시간 복잡도는 $O(N^3)$ 이 되지요. 4.2절에서 이동 평균을 빠르게 계산하기 위해 사용했던 변환을 이용해 이 알고리즘을 $O(N^2)$ 시간에 수행되도록 개선할 수 있습니다. 코드 4.9의 betterMaxSum()이 이 구현을 보여줍니다. $O(N)$번 수행되는 반복문이 두 개 겹쳐 있으니 이 알고리즘의 시간 복잡도는 O (N2 )이 됨을 쉽게 알 수 있습니다.

코드 4.9 최대 연속 부분 구간 합 문제를 푸는 무식한 알고리즘들

const int MIN = numeric_limits<int>::min();
// A[] 의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: $O(N^3)$
int inefficientMaxSum(const vector<int>& A) {
     int N = A.size(), ret = MIN;
     for(int i = 0; i < N; ++i)
         for(int j = i; j < N; ++j) {
            // 구간 A[i..j]의 합을 구한다.
             int sum = 0;
             for(int k = i; k <= j; ++k)
                 sum += A[k];
             ret = max(ret, sum);
        }
    return ret;
}

// A[] 의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: $O(N^2)$
int betterMaxSum(const vector<int>& A) {
     int N = A.size(), ret = MIN;
     for(int i = 0; i < N; ++i) {
         int sum = 0;
         for(int j = i; j < N; ++j) {
            // 구간 A[i..j]의 합을 구한다.
            sum += A[j];
            ret = max(ret, sum);
        }
    }
    return ret;
}

7장에서 다루는 분할 정복 기법을 이용하면 이보다 빠른 시간에 동작하는 알고리즘을 설계할 수 있습니다. 입력받은 배열을 우선 절반으로 잘라 왼쪽 배열과 오른쪽 배열로 나눕니다. 이때 우리가 원하는 최대 합 부분 구간은 두 배열 중 하나에 속해 있을 수도 있고, 두 배열 사이에 걸쳐 있을 수도 있습니다. 이때 각 경우의 답을 재귀 호출과 탐욕법을 이용해 계산하면 훌륭한 분할 정복 알고리즘이 되지요. 코드 4.10은 이런 알고리즘의 구현을 보여줍니다. 7장에서는 이런 알고리즘의 시간 복잡도를 분석하는 방법을 소개하는데, 이 방법대로 분석해 보면 이 알고리즘의 시간 복잡도는 O (NlgN)이 됩니다.

코드 4.10 최대 연속 부분 구간 합 문제를 푸는 분할 정복 알고리즘

// A[lo..hi]의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: O(nlgn)
int fastMaxSum(const vector<int>& A, int lo, int hi) {
    // 기저 사례: 구간의 길이가 1일 경우
    if(lo == hi) return A[lo];
    // 배열을 A[lo..mid], A[mid+1..hi]의 두 조각으로 나눈다.
    int mid = (lo + hi) / 2;
    // 두 부분에 모두 걸쳐 있는 최대 합 구간을 찾는다. 이 구간은
    // A[i..mid]와 A[mid+1..j] 형태를 갖는 구간의 합으로 이루어진다.
    // A[i..mid] 형태를 갖는 최대 구간을 찾는다.
    int left = MIN, right = MIN, sum = 0;
    for(int i = mid; i >= lo; --i) {
        sum += A[i];
        left = max(left, sum);
    }
    // A[mid+1..j] 형태를 갖는 최대 구간을 찾는다.
    sum = 0;
    for(int j = mid+1; j <= hi; ++j) {
        sum += A[j];
        right = max(right, sum);
    }
    // 최대 구간이 두 조각 중 하나에만 속해 있는 경우의 답을 재귀 호출로 찾는다.
    int single = max(fastMaxSum(A, lo, mid),fastMaxSum(A, mid+1, hi));
    // 두 경우 중 최대치를 반환한다.
    return max(left + right, single);
}

마지막으로 이 문제를 선형 시간에 푸는 방법은 8장에서 다루는 동적 계획법을 사용하는 것입니다. $A[i]$를 오른쪽 끝으로 갖는 구간의 최대 합을 반환하는 함수 $maxAt(i)$를 정의해 봅시다. 그런데 $A[i]$에서 끝나는 최대 합 부분 구간은 항상 $A[i]$ 하나만으로 구성되어 있거나, $A[i - 1]$를 오른쪽 끝으로 갖는 최대 합 부분 구간의 오른쪽에 $A[i]$를 붙인 형태로 구성되어 있음을 증명할 수 있습니다. 따라서 $maxAt()$을 다음과 같은 점화식으로 표현할 수 있게 됩니다.

$$ maxAt(i) = \max(0, maxAt(i - 1)) + A[i] $$

이 식을 반복적 동적 계획법으로 구현한 것이 코드 4.11입니다. 이 코드는 딱 하나의 반복문을 갖고 있기 때문에, 시간 복잡도는 $O(N)$이 됩니다.

코드 4.11 최대 연속 부분 구간 합 문제를 푸는 동적 계획법 알고리즘 

// A[] 의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: O(n)
int fastestMaxSum(const vector<int>& A) {
    int N = A.size(), ret = MIN, psum = 0;
    for(int i = 0; i < N; ++i) {
        psum = max(psum, 0) + A[i];
        ret = max(psum, ret);
    }
    return ret;
}

이렇게 각각 $O(N^3)$, $O(N^2)$, $O(N \lg N)$, 그리고 $O(N)$의 시간 복잡도를 갖는 네 개의 알고리즘을 제시했습니다. 이제 각 알고리즘의 수행 시간을 짐작해 봅시다. 각 테스트 케이스별 시간 제한이 1초이고 N의 상한이 1,000, 10,000, 그리고 100,000일 때 이 중 어떤 알고리즘을 사용할 수 있을까요?

  • ᆞN = 1,000: 이 때 $N^3$은 10억으로 주먹구구 법칙의 기준을 넘어서므로 ,$O(N^3)$ 알고리즘을 사용할 때는 우선 주의하는 것이 좋습니다. 하지만 반복문의 내부가 아주 단순하기 때문에 아마도 시간 안에 수행할 수 있을 거라고 짐작됩니다. 다른 세 개의 더 빠른 알고리즘은 별 무리 없이 수행할 수 있겠지요.
  • ᆞN = 10,000: 이때 $N^3$은 기준의 1만 배인 1조이므로 O (N3 ) 알고리즘은 시간 안에 돌아갈 가능성이 거의 없습니다. 반면 $O(N^2)$은 어떨까요? 이때 $N^2$는 1억 정도이므로 주의해야 할 범위에 들어갑니다. 그러나 이 알고리즘의 반복문 내부도 엄청나게 단순하기 때문에 아마도 충분히 시간 안에 돌아갈 거란 생각이 듭니다. 그러면 그보다 빠른 두 알고리즘은 문제없이 수행되겠지요.
  • ᆞN = 100,000: 이때는 $N^2$도 기준의 백 배인 100억이 됩니다. 따라서 $O(N^2)$ 알고리즘도 시간 안에 돌아갈 가능성이 높지 않습니다. 반면 $N \lg N$는 대략 2천만 정도이므로 다른 두 알고리즘은 시간 안에 수월하게 돌아갈 겁니다.

과연 우리 짐작이 모두 맞을까요? 그림 4.5는 임의로 생성한 해당 크기의 입력에 대해 네 알고리즘의 수행 시간을 보여줍니다.2 입력의 크기는 오른쪽으로 한 칸 갈 때마다 두 배씩 늘어난다는 점에 유의하세요. 1초 안에 처리할 수 있는 최대 입력 크기가 각 알고리즘에 따라 어떻게 변하는지 살펴봅시다.

그림 4.5 최대 연속 부분 구간 합 문제를 푸는 알고리즘의 속도 비교

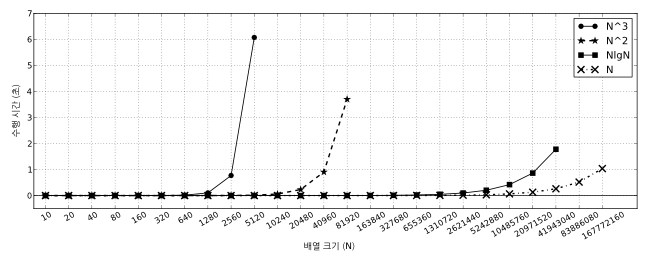
  • $O(N^3)$ 알고리즘: 크기 2560인 입력까지를 1초 안에 풀 수 있습니다. 이때 $2560^3$은 대략 16억입니다.
  • ᆞ$O(N^2)$ 알고리즘: 크기 40960인 입력까지를 1초 안에 풀 수 있습니다. 이때 $40960^2$은 대략 16억입니다.
  • ᆞ$O(N \lg N)$ 알고리즘: 크기가 대략 2천만인 입력까지를 1초 안에 풀 수 있습니다. 이때 $N \lg N$은 대략 5억입니다.
  • $O(N)$ 알고리즘: 크기가 대략 1억 6천만인 입력까지를 1초 안에 풀 수 있습니다.

다행히 위의 세 경우 모두 우리의 예상이 맞았음을 알 수 있지요. 특히 중요한 것은 주먹구구 법칙으로 예측한 것보다 느리게 동작하는 프로그램은 없었다는 점입니다. 1억이라는 기준은 가능한 보수적으로 정한 것이기 때문에 이 현상은 바람직한 것입니다. 당연히 돌아갈 거라고 믿고 프로그램을 짰는데 너무 느린 것보다는, 시간 초과할 가능성이 있을 때 미리미리 조심하는 쪽이 나으니까요.

이 결과에서는 1초 내에 수행할 수 있는 반복문의 수행 횟수가 알고리즘 간에 최대 열 배까지 차이나는 것도 볼 수 있습니다. 굉장히 단순한 반복문 내부, 시간 복잡도 분석 과정에서 생략된 상수 등이 이런 결과를 불러왔을 거라고 짐작할 수 있지요.

  1. 물론 시간이 지날수록 CPU는 빨라지므로 1억이라는 숫자는 갈수록 커질 것입니다. 그러나 하드웨어의 속도는 아주 천천히 증가하고, 어차피 이 법칙 자체가 근사값이기 때문에 1억이란 기준은 현재까지는 유효한 것 같습니다. ↩

  2. 실험 환경은 인텔 코어 i7 920 (네할렘), g++ 4.4.3, 우분투 리눅스 10.04입니다. ↩