28.10 다시 쓰기
아래는 859쪽(3쇄 기준)부터 시작하는 두 개의 꼭지(강결합 컴포넌트 분리를 위한 타잔의 알고리즘, 강결합 컴포넌트 분리 알고리즘의 구현)를 다시 쓴 것입니다.
강결합 컴포넌트 분리를 위한 타잔의 알고리즘
주어진 그래프를 SCC로 분할하는 간단한 방법은 모든 정점에서 한 번씩 깊이 우선 탐색을 수행하는 것입니다. 그러면 모든 정점 쌍에 대해 양방향 경로가 모두 있는지 쉽게 확인할 수 있지요. 하지만 이런 방법은 O(|V|×|E|) 시간을 필요로 하기 때문에 그래프가 커질 경우 사용할 수 없습니다. 강결합 컴포넌트 분리를 위한 타잔(Tarjan)의 알고리즘은 한 번의 깊이 우선 탐색으로 각 정점을 SCC별로 분리합니다. 타잔의 알고리즘은 유도하는 과정이 까다롭지만 깊이 우선 탐색을 써서 그래프 구조에 관한 문제를 푸는 아주 좋은 예입니다.
우선 임의의 정점에서부터 깊이 우선 탐색을 수행해 DFS 스패닝 트리를 만듭시다. 그림 28.12(b)는 (a)에 주어진 그래프의 가장 왼쪽 정점에서 깊이 우선 탐색을 해서 얻을 수 있는 스패닝 트리를 보여줍니다. 이 그림에서 주목할 부분은 이 스패닝 트리를 적절히 자르기만 해도 정점들을 SCC로 분리할 수 있다는 점입니다. 우연일까요? 그렇지 않음을 어렵지 않게 증명할 수 있습니다. 깊이 우선 탐색이 어떤 SCC를 처음 방문했다고 합시다. 이 정점을 x라고 하지요. 한 SCC에 속한 두 정점 간에는 항상 경로가 있기 때문에, 깊이 우선 탐색은 dfs(x)가 종료하기 전에 같은 SCC에 속한 정점을 전부 방문하게 될 겁니다. 따라서 이 SCC에 속한 정점들은 모두 x를 루트로 하는 서브트리에 포함됩니다. 이때 스패닝 트리를 잘라서 SCC를 분리할 수 없는 유일한 경우는 x와 같은 SCC에 속한 정점 y 사이에 다른 정점 z가 끼어 있는 경우 뿐입니다. 그러나 이 경우 z에서 y 로 가는 경로와 y에서 x로 가는 경로를 합치면 z에서 x로 가는 경로를 만들 수 있습니다. 따라서 z는 x와 같은 SCC에 속해야 하고, 원래의 가정이 모순이 됨을 알 수 있지요.
타잔의 알고리즘은 깊이 우선 탐색을 수행하면서 각 정점들을 SCC로 묶습니다. 이를 위해 간선을 따라 재귀 호출이 반환될 때마다 이 간선을 자를지 여부를 결정합니다. 해당 간선을 타고 내려가는 시점이 아니라, 반환되는 시점에 간선을 자르는 것에 유의하세요. 탐색을 수행하면서 각 서브트리에 대한 정보를 수집한 후에야 간선을 자를지 말지 결정할 수 있기 때문입니다. 만약 간선을 자르기로 하면, 하나의 SCC를 새로 만듭니다. 어떤 정점 v를 루트로 하는 서브트리를 탐색한 뒤, 그 부모인 u로 재귀호출을 반환하면서 트리 간선 (u,v)를 자르기로 결정했다고 합시다. v를 루트로 하는 서브트리는 모두 탐색한 후이므로, 이 서브트리의 어떤 간선을 잘라야 할지 이미 모두 파악한 상태입니다. 타잔 알고리즘은 아직 잘리지 않은 간선으로 v와 연결된 정점들을 모두 모아서 하나의 SCC로 묶어 줍니다.
그러면 이제 각 간선을 자를지 여부를 정해 봅시다. 트리 간선 (u,v)를 자른다는 것은 v에서 u로 갈 수 있는 경로가 없다는 뜻입니다. v에서 u로 가는 경로에는 항상 역방향 간선이 하나 이상 포함되어 있어야 하므로, 이 점을 이용합시다. 절단점 판단 알고리즘과 같이, v를 루트로 하는 서브트리를 탐색하면서 만나는 역방향 간선을 거쳐 닿을 수 있는 가장 높은 정점을 찾습니다. 이 정점이 u 혹은 그보다 높이 있는 정점이라면 이 역방향 간선을 통해 v에서 u로 갈 수 있고, 따라서 간선 (u,v)를 잘라선 안 됩니다.
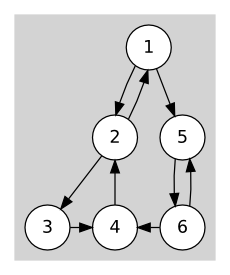
이대로 끝인 것 같지만, 아직 고려해야 할 점이 있습니다. 절단점 판단 알고리즘은 무향 그래프에 대해 동작했으므로 역방향 간선만 신경쓰면 됐지만, 방향 그래프를 다루는 SCC 분리 문제에서는 교차 간선을 신경써야 하기 때문입니다. 실제로 v를 루트로 하는 서브트리에서 밖으로 나가는 역방향 간선이 하나도 없더라도, (u,v)를 자를 수 없는 경우가 있습니다. 그림 28.13 (a)가 이런 경우를 보여줍니다. 1번 정점에서 깊이 우선 탐색을 시작해, 2, 3, 4번 정점을 순서대로 방문하고 1번 정점으로 돌아왔다가 5, 6번 정점을 방문했다고 합시다. 5를 루트로 하는 서브트리에서 밖으로 나가는 역방향 간선은 없지만, 교차 간선 (6,4)를 이용하면 5번에서 그 부모인 1번으로 가는 경로를 찾을 수 있기 때문에 (1,5)를 잘라서는 안 됩니다. 하지만 모든 교차 간선을 사용해 선조로 올라갈 수 있는 것은 아닙니다. 그림 28.13 (b)는 이런 경우를 보여줍니다. 여기서는 간선 (6,4)를 통해도 1번으로 가는 경로를 찾을 수 없으므로, (1,5)를 자르게 됩니다.
그림 28.13 강결합 컴포넌트 분리와 교차 간선
(eps 버전)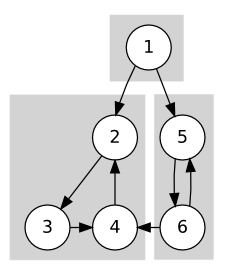
(eps 버전)(a) (b)
이 두 경우를 어떻게 구분할 수 있을까요? 그림 28.13의 두 그래프에서 교차 간선 (6,4)를 따라가면 4번 정점을 만납니다. 4번 정점을 이용해 1번 정점으로 가려면, 4번에서 1번으로 올라가는 경로 중 끊어지는 간선이 하나도 없어야 합니다. 그런데 끊어지는 간선이 하나라도 있을 경우 4번은 이미 이 간선이 끊어지면서 별도의 SCC로 묶였을 것입니다. 이미 2번 정점을 루트로 하는 서브트리의 탐색은 끝난 뒤이기 때문입니다. 따라서 교차 간선을 따라가 만난 정점이 이미 SCC로 묶여 있는지 여부를 이용하면 이 교차 간선을 통해 조상으로 올라갈 수 있는지를 판단할 수 있습니다.
이제 트리 간선 (u,v)를 끊을 수 없는 경우가 언제인지 알 수 있습니다. v를 루트로 하는 서브트리에서, v보다 먼저 발견된 정점으로 가는 역방향 간선이 있다면 (u,v)를 끊어선 안 됩니다. 그런 역방향 간선이 없다고 해도, v보다 먼저 발견되었으면서 아직 SCC로 묶여 있지 않은 정점으로 가는 교차 간선이 있다면 (u,v)를 끊어선 안 됩니다.
강결합 컴포넌트 분리 알고리즘의 구현
이와 같이 구현된 SCC 분리 알고리즘의 구현을 코드 28.10에서 볼 수 있습니다. scc()가 실제 깊이 우선 탐색을 구현하는 부분이고, tarjanSCC()는 배열과 카운터를 초기화하고 scc() 함수를 호출해 줍니다.
코드 28.10: 타잔의 강결합 컴포넌트 분리 알고리즘의 구현
// 그래프의 인접 리스트 표현 vector<vector<int> > adj; // 각 정점의 컴포넌트 번호. 컴포넌트 번호는 0 부터 시작하며, // 같은 강결합 컴포넌트에 속한 정점들의 컴포넌트 번호가 같다. vector<int> sccId; // 각 정점의 발견 순서 vector<int> discovered; // 정점의 번호를 담는 스택 stack<int> st; int sccCounter, vertexCounter; // here를 루트로 하는 서브트리에서 역방향 간선이나 교차 간선을 // 통해 갈 수 있는 정점 중 최소 발견 순서를 반환한다. // (이미 SCC로 묶인 정점으로 연결된 교차 간선은 무시한다) int scc(int here) { int ret = discovered[here] = vertexCounter++; // 스택에 here 를 넣는다. here 의 후손들은 모두 스택에서 here 후에 들어간다. st.push(here); for(int i = 0; i < adj[here].size(); ++i) { int there = adj[here][i]; // (here,there) 가 트리 간선 if(discovered[there] == -1) ret = min(ret, scc(there)); // there가 무시해야 하는 교차 간선이 아니라면 else if(sccId[there] == -1) ret = min(ret, discovered[there]); } // here에서 부모로 올라가는 간선을 끊어야 할지 확인한다 if(ret == discovered[here]) { // here 를 루트로 하는 서브트리에 남아 있는 정점들을 전부 하나의 컴포넌트로 묶는다 while(true) { int t = st.top(); st.pop(); sccId[t] = sccCounter; if(t == here) break; } ++sccCounter; } return ret; } // tarjan 의 SCC 알고리즘 vector<int> tarjanSCC() { // 배열들을 전부 초기화 sccId = discovered = vector<int>(adj.size(), -1); // 카운터 초기화 sccCounter = vertexCounter = 0; // 모든 정점에 대해 scc() 호출 for(int i = 0; i < adj.size(); i++) if(discovered[i] == -1) scc(i); return sccId; }
이 알고리즘에서 눈여겨볼 부분은 현재 위치를 루트로 하는 서브트리에 남아 있는 정점들을 모두 찾는 방법입니다. here에서 부모로 올라가는 간선을 끊기로 결정하면, 서브트리에 남아 있는 정점들을 모두 한 SCC로 묶은 뒤 이들을 그래프에서 지워 버려야 하지요. 이 알고리즘은 이 번거로운 작업을 하는 대신 스택을 이용합니다.
scc()는 깊이 우선 탐색 과정에서 방문한 정점들의 번호를 담는 스택을 유지합니다. 이 스택은 지금까지 방문한 정점 중 아직 SCC로 묶이지 않은 모든 정점들의 번호를 갖습니다. 각 정점을 처음 방문할 때마다 스택에 해당 정점의 번호를 집어넣기 때문에, 스택에서 here 위에 들어있는 정점들은 모두 here의 후손들입니다. 따라서 스택을 이용하면 here의 후손이면서 아직 다른 SCC로 묶이지 않은 정점들을 쉽게 얻을 수 있습니다. here를 만날 때까지 계속 스택에서 정점을 꺼내면 되니까요.
또 하나 눈여겨볼 만한 부분은 scc() 내에서 역방향 간선, 순방향 간선, 그리고 SCC로 묶이지 않은 교차 간선 간의 구분을 하지 않은 것입니다. 각 경우에 필요한 동작들을 살펴 보면 이들을 서로 구분할 필요가 없다는 것을 쉽게 알 수 있습니다.
scc()가 깊이 우선 탐색과 다른 것은 스택에서 정점을 꺼내는 반복문 뿐인데, 분할 상환 분석을 이용해 이 반복문의 총 수행 회수가 O(|V|)라는 것을 보일 수 있지요. 따라서 이 알고리즘의 시간 복잡도 또한 O (|V| + |E|)가 됩니다.